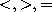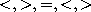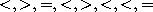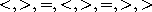Monotonicity 2

Memory limit: 256 MB

This task is a harder version of task Monotonicity from the third stage of 17th Polish OI. It wasn't used in the contest itself.

For an integer sequence 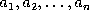we define its monotonicity scheme as the sequence 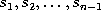of symbols , 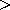or . The symbol 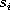represents the relation between 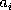and 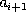. For example, the monotonicity scheme of the sequence 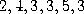is .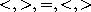

We say that an integer sequence 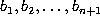with monotonicity scheme 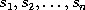, realizes another monotonicity scheme 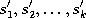if for every 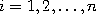it holds that 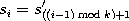. In other words, the sequence 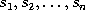can be obtained by repeating the sequ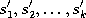ence and removing appropriate suffix from that repetition. For example, the sequence 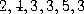realizes each and every one of the following schemes:

An integer sequence 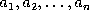and a monotonicity scheme 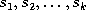are given. Your task is to find the longest subsequence 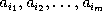(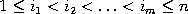) of the former that realizes the latter.

Input

The first line of the standard input holds two integers and 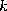(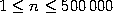, 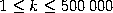), separated by a single space, denoting the lengths of the sequences 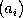and monotonicity scheme 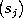respectively.

The second input line gives the sequence 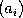, i.e, it holds integers 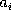separated by single spaces ().

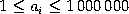Finally, the third lines gives the monotonicity scheme 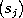, i.e., it holds 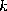symbols 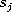of the form <, > or = separated by single spaces.

Output

In the first line of the standard output your program should print out a single integer 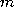, the maximum length of a subsequence of 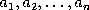that realizes the scheme .

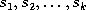In the second line it should print out any such subsequence 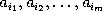, separating its elements by single spaces.

Example

For the input data:

7 3
2 4 3 1 3 5 3
< > =

the correct result is:

6
2 4 3 3 5 3

Task authors: Marian M. Kedzierski, Piotr Niedzwiedz.